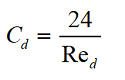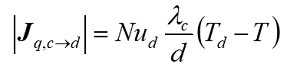And an example FlowVision project: "Simulation of flow of water with sand"
How to model particles?
If you find yourself asking this question, then you should know that we and the FlowVision user guide are with you. On a more serious note, the topic of modelling dispersed phases has already indirectly come up in articles on multiphase flows and icing. And the non-trivial examples of coal combustion and droplet evaporation have been covered step-by-step in the tutorial.
Nevertheless, dispersed problems are diverse and hold many questions. It's time to bring clarity to particle modelling! Over the course of our dive into the topic of dispersion, we will focus on key settings, talk about the current capabilities and limitations of FlowVision, and examine projects "from the inside".
HOW DOES THE DISPERSION CYCLE WORK?
When approaching the topic of dispersion, it’s best to eat the elephant one bite at a time.
- This article will cover particles in the context of general physics. Here we will examine the approach implemented by the FlowVision dispersion solver, define the classes of problems able to be solved, note existing constraints, and together we will simulate a dispersed flow (using example: flow of water with sand).
- The next article will focus on modelling bubbles and droplet fragmentation.
- The final part will be devoted to the modelling of flows through porous media.
Of course, we will not leave you without examples of real FlowVision projects. They will definitely make it easier to move away from abstract concepts and dive straight into modelling. Should you have any questions, do not hesitate to send them to the tech support team via email (support@flowvisioncfd.com).
Introduction to Particles
Let's start with the definitions
Dispersed medium – refers to either small particles in a gaseous, liquid or solid aggregate state, or a solid with cavities (pores). Visions of humid sea-side air, sandy beaches and a glass of lemonade evoke thoughts of summer, but are also demonstrative examples of dispersed media. In these examples we can see the key feature of these media - particles do not exist on their own, but rather interact with the continuous phase carrying them:
- water droplets are carried by the air flow
- gas bubbles float in the drink
- water seeps through the sand into the ground
Furthermore, the particles are evenly distributed amongst the molecules of the continuous phase, without entering into a chemical reaction with them.
The interactions of the dispersed and continuous phases form a dispersed multiphase system. Based on the particle size (d), we can distinguish between coarse and fine dispersed systems. And if the particle diameter is similar to the size of the molecules of the carrier medium, then such a system is dubbed a true solution. It is not at all necessary for all particles in a dispersed system to have the same size and shape. On the contrary, they will most likely be completely unlike each other.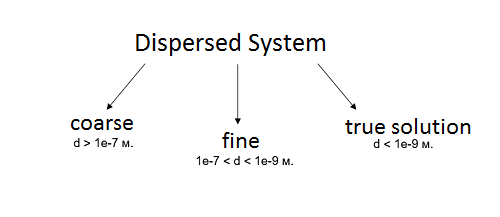 In FlowVision, the assumption is made that the particle size is always much larger than the molecule size. Under the initial and boundary conditions, the user can choose to model either identical particles (which have a specific average diameter), or a spectral distribution of particle sizes.
In FlowVision, the assumption is made that the particle size is always much larger than the molecule size. Under the initial and boundary conditions, the user can choose to model either identical particles (which have a specific average diameter), or a spectral distribution of particle sizes.
Dispersion in FlowVision: Particles and Carcass
Depending on the aggregate states of the dispersed and carrier phases, different dispersed systems are formed. All their diversity is displayed in the following table: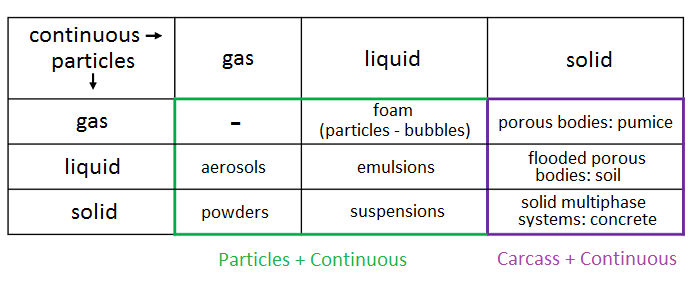 In FlowVision, dispersion in gaseous and liquid media is defined by the interaction of "Particles + Continuous", and flow through a solid porous medium is defined by the interaction "Carcass + Continuous".
In FlowVision, dispersion in gaseous and liquid media is defined by the interaction of "Particles + Continuous", and flow through a solid porous medium is defined by the interaction "Carcass + Continuous".
So what's the difference?
Conceptually, the phases "Particles" and "Carcass" are similar - within the framework of the Euler method, each can be considered to be a continuum. However, the physics for these two phases are different. The main difference is that the "Carcass" phase is rigid. It follows that the models and relationships applied to particles and rigid bodies are different: the physical process equations for a Carcass do not have a convective term. And anyway, the equations for Motion and Phase Transfer are pretty much irrelevant for a Carcass.
At this stage, let's follow the example set by our developers and split our account of FlowVision’s dispersion capabilities into two parts: Particles and Carcass. From here on the sole focus of the article will be the Particles. The use of a Carcass for modelling heat exchangers, filters, soil and other porous media, will be covered in the third article of this series.
Euler's Method in Particle Modelling
In FlowVision, the particles being considered are combined into a dispersion cloud. Thus, physical processes are not evaluated for each individual particle, but rather for a volume of space, which has the properties of a continuous medium. Therefore, when simulating a multiphase flow, the cloud of particles and the continuous carrier phase interact as interpenetrating continuous media.
However, this approach does not explicitly take into account the collisions of particles with each other and, as a result, there are no stresses inside the cloud. Therefore, it is typical to introduce additional models (e.g. fluidized bed model) in order to account for this interaction of particles with each other within the framework of the Euler method. FlowVision implements a simple repulsion model that introduces an additional term to the particle motion equation. It’s coefficients can be edited within the FlowVision interface.
Why does the dispersion solver use Euler's method?
Another approach to modelling particles in a continuous medium is the Lagrange method. It involves solving a larger number of equations for the modelled particles. Each modelled particle represents a certain (fairly large) number of real particles. The Lagrangian solver records the movement of these model particles from one face to the next for each cell through which the particle trajectory passes. The Lagrangian method had been implemented in the 2nd generation of FlowVision. But as of FlowVision 3.xx.xx it was decided to switch to the Euler method, which requires less computational resources and less RAM. Both methods (Euler and Lagrange) have their advantages and disadvantages. A detailed overview of these can be found in literature on the subject.
What is FlowVision able to simulate using particles?
- Multiphase dispersed flows: aerosols, powders, emulsions, suspensions
- The movement of gas bubbles in a liquid (taking into account the change in size of the bubbles)
- Evaporation of liquid droplets
- Combustion of coal and similar substances that separate into water, coke, and ash
- Jet spraying from a nozzle (taking into account the splitting and merging of drops)
- Surface icing
Limitations
- The current implementation in FlowVision does not support the adding of more than one dispersed phase to a model (i.e. each model is limited to only one Particles or only one Carcass phase).
- FlowVision is not yet able to model the phase transition of a continuous phase changing to a dispersed one.
Aside from limitations, there are also strong capabilities:
- Particles can participate in multiphase VOF interactions: (particles + continuous #1) + continuous #2.
- FlowVision 3.12.02 introduced a model for particle condensation. Condensation modelling is currently in beta testing, so if you encounter any difficulties in applying the model, please contact technical support: support@flowvisioncfd.com.
- Particles are compatible with periodic boundary conditions and sliding surfaces.
Dispersed flows: step-by-step
Dispersed flows are one of the more extensive and therefore most popular classes of dispersion problems among users. (Problems with disperse decomposition, icing, and coal combustion are also popular, but to a lesser extent). Fogs, aerosols, powders, solid admixtures, suspensions (cement mortar, orange juice) and emulsions (bitumen, milk) - all these substances surround us not only in industry, but also in everyday life. Let's move from theory to practice and add particles to the laminar pipe-flow tutorial. Instead of water flowing through the pipe, let it now be a suspension of sand (SiO2) in water. Here we will go over the most important of them:
- Number of size groups in the spectrum
- Physical processes in the dispersed phase
- Particle cloud drag coefficient
- Nusselt number
- Dispersion settings on BCs
- Multiphase D
- Variables in the Postprocessor
JUST ADD PARTICLES
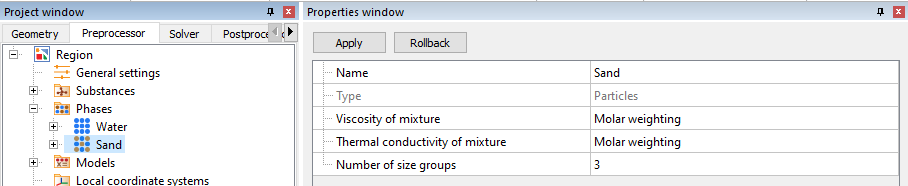
Start modelling dispersed flows by creating a "Particles" phase where you are immediately taken to the key settings: Particles> Number of size groups.
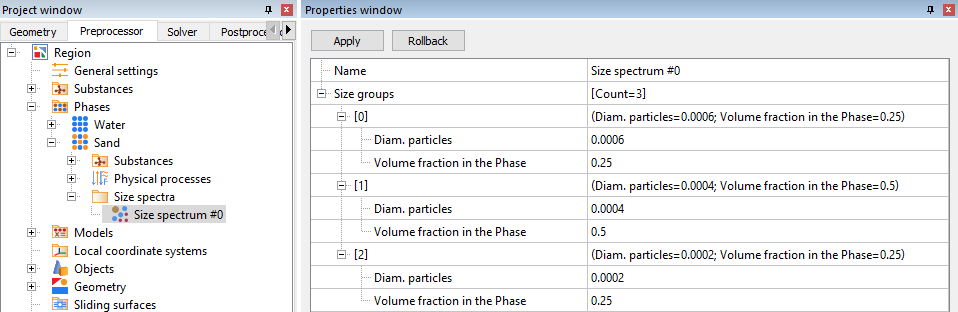
Then create a Size Spectrum, which will consist of three size groups with different diameters. Of course, it is worth keeping in mind that the sum of the volume fractions of all groups = 1.
One phase can contain up to a maximum of 100 different size groups.
It is unlikely that you would need more than this. The limit on the number of groups is linked to the capabilities of computing machines: for each (out of 100!) size groups, there needs to be allocated a certain amount of RAM, which in modern realities is not an unlimited resource.
PHYSICAL PROCESSES
Let's give a more detailed definition of the scenario being simulated. Let hot sand (T = 50°C) and cold water (T = 0°C) enter through the pipe inlet with a ratio of 1:4. Furthermore, let’s assign three distinct groups of sand grains with sizes (d1 < d2 < d3) in a ratio of 1:2:1. This mixture of water and sand, intermixes further as it flows through the pipe and exits at the other end.
 For modelling, we take into account the following processes:
For modelling, we take into account the following processes:
- Heat transfer in the dispersed phase (as part of the heat exchange process between the dispersed medium and the continuous phases) > heat transfer = convection and conduction
- Transfer of particles of different diameters within the dispersed phase > phase transfer = convection and diffusion
- Motion of the particle cloud within the continuous phase > motion
PARTICLE DRAG COEFFICIENT
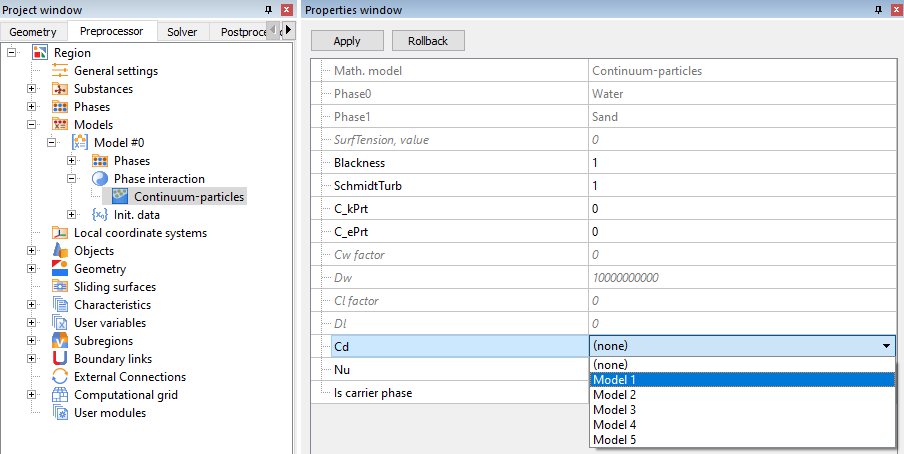
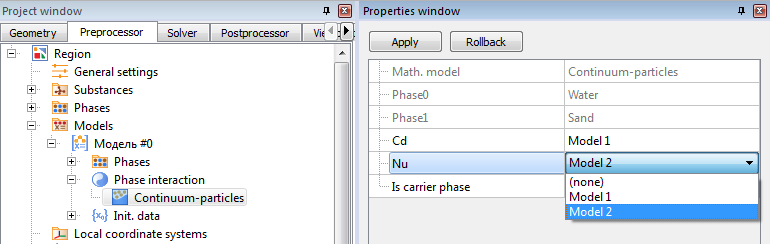
Model > Phase interaction > Continuum - Particles > Сd
To calculate the drag coefficient of particles, select one of the five models.
The drag coefficient (Cd) for the dispersion cloud is determined by the environment through which it flows. For a continuous phase (Knudsen number, Kn < 0.001), the focus is typically on the dependence of drag coefficient on Reynolds number, Re.
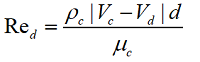 Parameters with index "c" are parameters of the continuous medium, and those with index "d" are parameters of the dispersed medium.
Parameters with index "c" are parameters of the continuous medium, and those with index "d" are parameters of the dispersed medium.
The first scientist to propose that the coefficient of resistance is dependent on the Reynolds number was Sir George Gabriel Stokes. The relationship he derived is in excellent agreement with experimental data for Re <0.1.
- Models 1, 2 are close to Stokes flow, where particles have low velocity relative to the overall flow.
- Models 3, 4 were developed based on the works of (Ergun/Wen and Yu) and (Cheng), respectively, and allow the range of Re numbers of dispersed particles to be expanded up to Re < 3⋅105. These models work well for simulating the spraying of particles within a stationary domain.
- Model 5 is used in bubble modelling. Read more about this process in the next article on dispersion.
NUSSELT NUMBER
Model > Phase interaction > Continuum - Particles > Nu
To calculate the Nusselt number for the particles, select one of the two models.
The Nusselt number (Nu) describes the ratio between the convective and conductive heat transfer and is used to determine the heat flux:
- Model 1 is more universal, and is suitable for modelling the joint movement of particles in a stream, and the movement of particles in a stationary environment.
- Model 2 is split into two expressions for calculations at low and high Re numbers.
DISPERSION SETTINGS AT BOUNDARY CONDITIONS
For each of the selected physical processes, it is necessary to define the following properties of the dispersed phase at the boundary conditions:
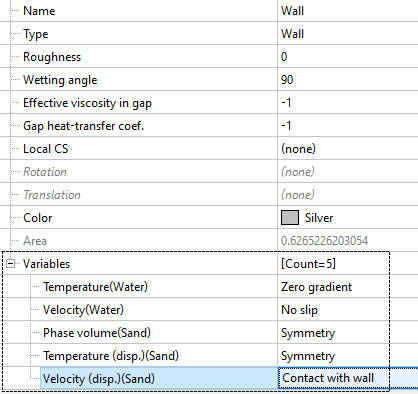
- Phase volume (Sand)
- Temperatures (disp.) (Sand)
- Velocities (disp.) (Sand)
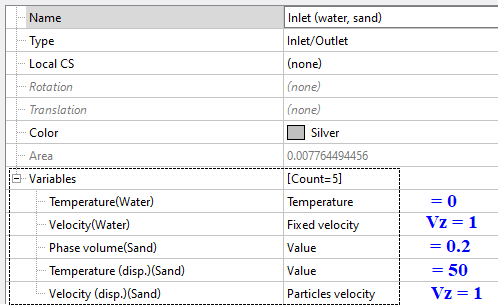
Inlet (Inlet/Outlet)
At the inlet we set values based on the provided data: we know the values for phase volume (= 1/5 = 0.2), temperature (= 50 when Tref. = 273) and velocity (= 1).
Provided the flow rate of particles over a BC is known, we can set either the volumetric velocity (Vd⋅φd) or the mass velocity (ρd⋅Vd⋅φd).
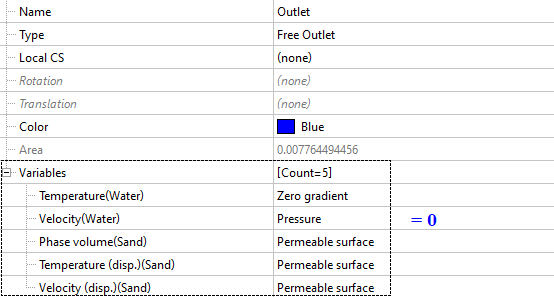
Outlet (Free outlet)
On the surface corresponding to the physical outlet, set the condition ‘permeable surface’ for all variables related to the dispersed phase. This ensures undisturbed flow for the dispersed phase. The permeable surface condition is analogous to the zero gradient condition for the continuous phase. For water, we also ensure the undisturbed outflow of the medium by setting the pressure value to zero.
If the outlet flow rate or outlet parameters are known, then you can also set fixed values for the dispersed phase variables at the outlet BC.
Pipe surface (wall)
At the pipe walls, the velocity is described using the condition contact with wall, which you can use to vary the direction in which particles rebound off the wall.
If you are modelling membranes, then FlowVision allows you to assign a permeable wall condition: set the values for phase volume, temperature, and velocity (just like for an inlet BC), and for the continuous phase leave the condition of no flow through the walls.
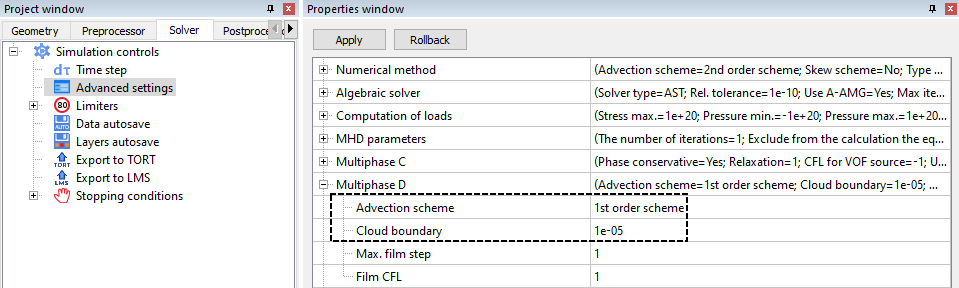
MULTIPHASE D
Dispersed multiphase settings are located under the Solver tab > Advanced settings.
The maximum film step and film CFL are only used when modelling icing. In this sense, Advection Scheme and Cloud Boundary are the more universally used dispersion parameters.
- Empirically, it has been determined that, in the current FlowVision implementation, using 1st order accuracy for the advection scheme leads to a more stable solution.
- The cloud boundary defines the lower limit for the value of the dispersed phase in a cell. If the actual phase value is less than the cloud boundary, then the particles in this cell are excluded from the calculation. By default, the cloud boundary value is 1e-5.
POSTPROCESSING: DISPERSED PHASE VARIABLES
The complete list of dispersed variables is displayed when you select the category Variables of phase “Sand”. Let's consider the ones typically used:
- Concentration [m-3] – the number of particles in a cell
- Phase volume [-] – the share of a cell occupied by the dispersed phase
- Velocity (disp.) [m/s] and Temperature (disp.) [K] relate to the dispersed phase only. The respective variables for the continuous phase are labelled Velocity and Temperature.
The specific size group that particles belong to is shown by the index in the square brackets: [0, 1, or 2]
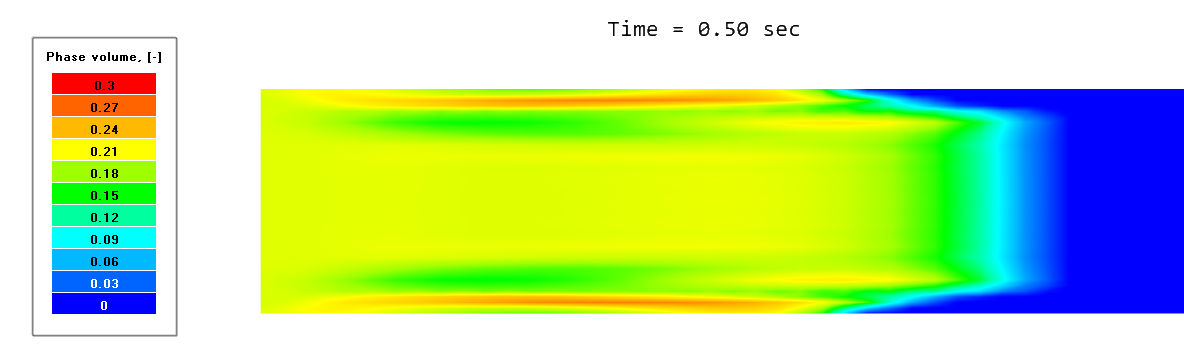
For example, phase volume indicates the total share of the dispersed phase, whereas phase volume [1] indicates the share of only the 1st group of particles (with diameter 0.0004 m). Let’s display the distribution of sand near the pipe inlet. To do this, we use the Variable of phase "Sand" > Phase Volume.
Summary
All this, concisely:
- Particles are elements of a medium and are completely independent from each other. This medium can be liquid (droplets), solid (grains of sand, dust grains, snowflakes) or gaseous (bubbles), and is separated by a separate continuous medium (liquid or gaseous), called the carrier phase. Different combinations of dispersed and continuous media form different dispersed systems, which are often familiar to us: dust in the air, bubbles in champagne, solid particles in a liquid (suspension), droplets in a liquid (emulsion).
- When modelling particles, FlowVision uses the Euler method. This makes it possible to optimize the use of computational resources in multiphase calculations by reducing the number of equations needed to be solved and the amount of RAM used.
- Currently, FlowVision is used to simulate:
- Multiphase dispersed flows: aerosols, powders, emulsions, suspensions
- The movement of gas bubbles in a liquid (taking into account the change in size of the bubbles)
- Evaporation of liquid droplets
- Combustion of coal and similar substances that separate into water, coke and ash
- Spraying a jet from a nozzle (taking into account the splitting and merging of drops)
- Surface icing
- The key stages in creating a project for modelling dispersed flow are:
-
- Determining the number of size groups in the spectrum of particles
- Specifying the physical processes for the dispersed phase
- Selecting a model for the drag coefficient of the cloud of particles
- Selecting a model for Nusselt number
- Dispersion settings on BCs
- Dispersion settings for advanced users
- Selecting variables for display in the PostProcessor