COMPUTATIONAL GRID AND MOVING BODIES: HOW DO THEY INTERACT DURING THE CALCULATION PROCESS?
FlowVision uses Euler's approach to mesh generation: the computational mesh is stationary, and the body moves along it.

Demonstration of Euler's approach: a "moving body" moving along the computational grid
First, the position of the object model is updated according to the applied laws of motion. Then, the object model geometry is subtracted from the computational grid. This process is repeated at each iteration.
The main difficulty in implementing this approach is that as the object moves through the space, cells of the computational grid disappear. But the fact that the mesh is not tied to the model geometry allows you to assign the body an absolutely arbitrary motion and simulate the full surface contact. Then, during the motion, the mesh is rebuilt only near the moving body, rather than over the entire volume of the computational space. This optimizes use of computational resources.
MOVING BODIES AND ADAPTATION
To resolve the near-wall layer of a body (whether it is moving or not), it is convenient and rational in terms of computational resources to apply mesh adaptation to the surface of this body. However, if you simply adapt the surface of a body that is in motion, then there will always be traces of adapted cells trailing behind it (as in the picture below). Merging will help remove unnecessary adaptation.
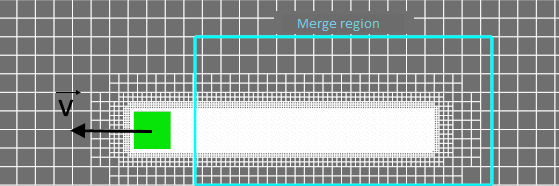
A trail of over-adaptation behind a moving cube. Use merging to optimize the computational mesh.
It is better to drain the trail of adaptation periodically, rather than at every step. Just like the unnecessary adaptation behind a moving body, frequent merging also consumes computational resources